Zahlen in der Tontechnik
Obwohl wir mit Audio arbeiten und unsere primären Werkzeuge zur Bewertung unsere Ohren sind, müssen wir manchmal auf Zahlen zurückgreifen, um den Klang zu beschreiben. Die meisten Spezifikationen basieren auf Zahlen. Bei der Aufzeichnung nutzen wir Zahlen zur Angabe der Datenmenge. Wenn wir einen Schalldruckpegel angeben wollen, nutzen wir Zahlen. Und damit ist noch nicht Schluss.

Dekade vs. Oktave
Bei der Beschreibung einer Dämpfung oder eines Pegelverlaufs bei einem Audiofilter wird allgemein die Angabe „dB pro Oktave“ genutzt, bspw. 6 dB pro Oktave oder kurz: 6 dB/Okt.
In anderen Bereichen der Elektronik beschreiben wir allerdings die Steigung pro Dekade, z.B. 20 dB pro Dekade.
Eine Oktave ist definiert als eine Verdopplung oder Halbierung eines Frequenzwerts. Eine Dekade ist das zehnfache (oder ein Zehntel von) einer beliebigen Größe (oder Frequenzbereich). Die Werte sind also jeweils nicht absolut, sondern relativ. Der wahrnehmbare Frequenzbereich des menschlichen Ohrs beträgt etwa zehn Oktaven oder drei Dekaden und reicht von etwa 20 Hz bis 20.000 Hz.
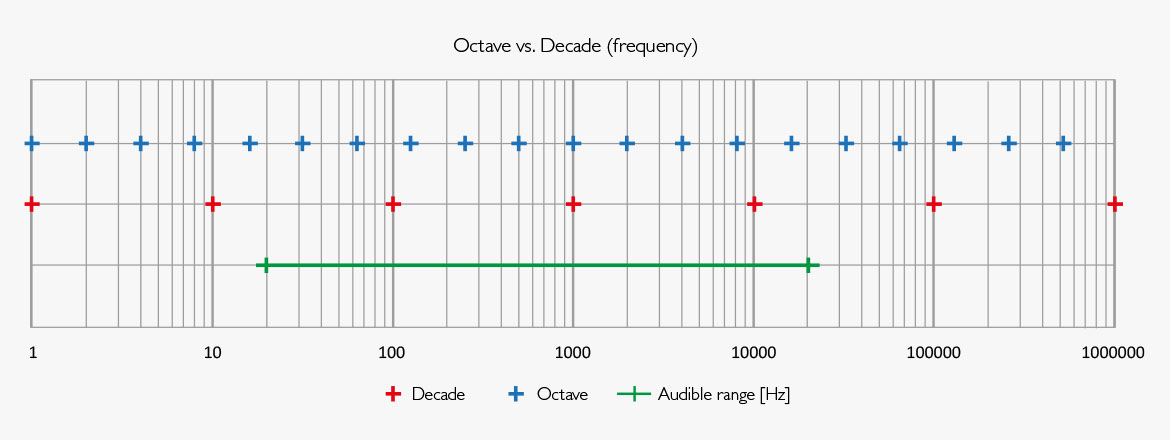
Abb. 1 Zahlenstrang markiert mit Oktav- und Dekadenintervallen.
Die Ordnung eines Filters definiert die Steilheit außerhalb seines Durchlassbereichs. Ein Filter erster Ordnung basiert in Prinzip auf einem elektronischen Bauteil, das einen frequenzabhängigen Widerstand aufweist. Dieses Bauteil ist meist eine Spule oder ein Kondensator in Verbindung mit einem Widerstand. Die Flankensteilheit beträgt je nach Konfiguration der beiden Komponenten ±6 dB pro Oktave. Ein Filter zweiter Ordnung enthält zwei dieser Komponenten in Kombination mit einem Widerstand, wie zwei Kondensatoren oder eine Spule und ein Kondensator. Die resultierende Flankensteilheit beträgt dann ±12 dB pro Oktave. Heutzutage sind diese Filter typischerweise nur in passiven Lautsprechern zu finden, während die meisten Filter digital über DSP realisiert werden.
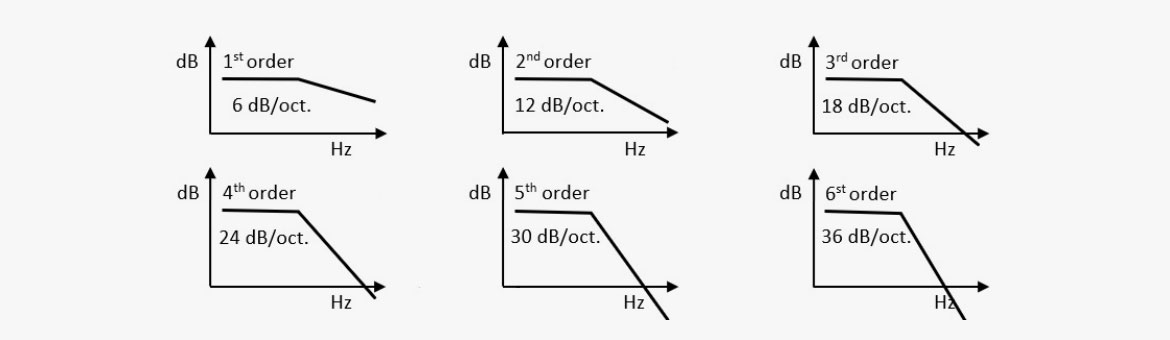
Die folgende Tabelle zeigt die Filterordnung und die zugehörige Flankensteilheit (hier Dämpfung) in dB/Okt. oder dB/Dekade.
| Filterordnung | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| dB/Oktave | 3 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| dB/Dekade | 10 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
Umrechnungstabelle: Filterflanken definiert durch Filterordnung, dB/Okt. oder dB/Dekade.
Lineare und logarithmische Skalen
Es gibt ein festes Intervall zwischen jeder Einheit der linearen Skala (z.B. 1, 2, 3, 4, wobei der Abstand zwischen jeder Einheit 1 ist).
Die logarithmische Skala hat ein festes Verhältnis zwischen den einzelnen Einheiten der Skala (z.B. Verhältnis 10 – die Einheiten sind 1 – 10 – 100 – 1000 usw., oder Verhältnis 2 – die Einheiten sind 1 – 2 – 4 – 8 – 16 usw.). Die logarithmische Skala findet Anwendung bei zahlreichen elektrischen oder akustischen Angaben, die zur Beschreibung von Mikrofonen verwendet werden (z.B. Volt, Pascal, etc.).
Der Mensch nimmt sowohl Pegel als auch Frequenz logarithmisch wahr. Bei der Frequenz lesen wir die Frequenzgangkurve über eine logarithmische Skala ab. Die Dezibel-Skala hängt mit der Art und Weise zusammen, wie der Mensch Pegel wahrnimmt. Somit entspricht die logarithmische Skala der Wahrnehmung eines gleichmäßigen Anstiegs.
Das Dezibel (dB)
Der Vorteil dieser Skala liegt darin, dass 1 dB ungefähr die geringste wahrnehmbare Pegeländerung darstellt. Eine Änderung des Pegels um 3 dB ist deutlich hörbar. 10 dB werden subjektiv als Verdopplung oder Halbierung empfunden. Im Großen und Ganzen wird jede Stufe der Skala als gleich groß wahrgenommen. Die signifikanteste dB-Angabe, die im wirklichen Leben auftritt, ist <200 dB, d.h. wenn der Wert dreistellig ist, ist die erste Ziffer stets eine „1“.
Die dB-Skala ist relativ. Somit kann jede Änderung in dB ausgedrückt werden. Eine Änderung von 0 dB ist überhaupt keine Änderung. Jeder positive dB-Wert zeigt eine positive Änderung an (der Wert steigt). Jeder negative dB-Wert zeigt eine negative Änderung an (der Wert sinkt).
Dezibel-Werte können als absolute Skala gelesen werden, wenn eine Referenz angegeben wird – zum Beispiel beim Schalldruckpegel, wo die Referenz 20 μPa beträgt (das entspricht etwa der Hörschwelle bei mittleren Frequenzen). Zur Beschreibung des Schalldruckpegels kann sowohl „dB re 20 μPa“ als auch „dB SPL“ (Sound Pressure Level / Schalldruckpegel) angegeben werden.
Eine weitere Referenz für elektrische Messungen ist 1 Volt, geschrieben als „o dBV“ oder „0 dB re 1 Volt“. Dieser absolute Wert gilt beispielsweise für die Angabe der Empfindlichkeit von Mikrofonen.
Bandbreite und Prozentsatz vs. Q
Parametrische Equalizer beinhalten typischerweise Glockenfilter als Bandbass- und Sperrfilter. Die Kontrollparameter sind Frequenz, Pegel und Q-Faktor oder Bandbreite. Bei Filtern, die für Messtechnik definiert sind, kann auch ein Prozentsatz zur Beschreibung der Bandbreite verwendet werden. Bandbreite, Q-Faktor und Prozentsatz drücken dasselbe aus. Welche Parameter angegeben werden, hängt jedoch von der Marke, dem Modell und der Anwendung ab. Bei einigen Geräten kann zwischen den Angaben umgeschaltet werden.
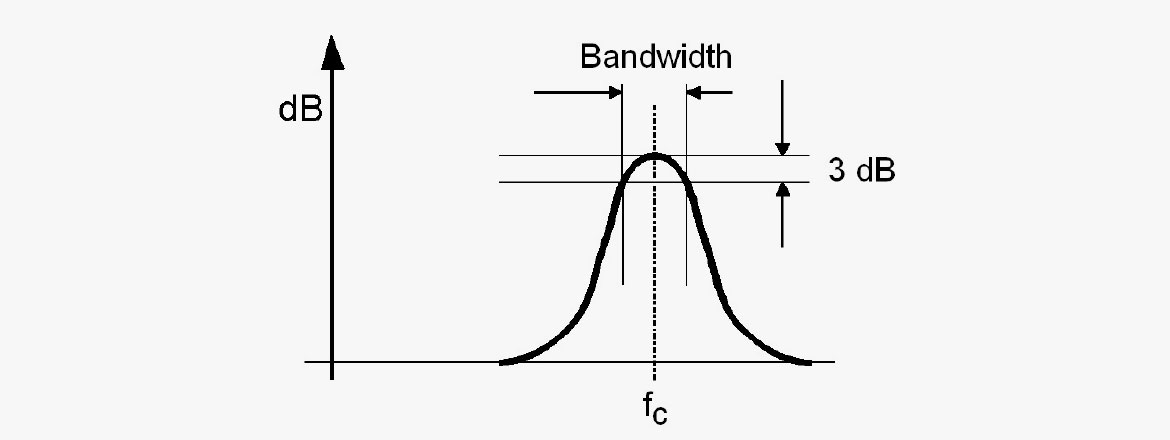
Im Folgenden erläutern wir die Zusammenhänge zwischen den verschiedenen Begriffen:
Bandbreite
Bandbreite ist die Frequenzspanne zwischen den -3dB Cutoff-Punkten auf einer Filterkurve, also fupper - flower [Hz]. Die Bandbreite wird entweder als absoluter Wert ([Hz] oder relativ in Oktaven ausgedrückt (oft 1/1 Oktave, 1/3 Oktave oder Bruchteile einer Oktave, ausgedrückt durch Dezimalzahlen wie z.B. 0,1 Oktaven).
Prozentsatz
Die Bandbreite ausgedrückt durch einen Prozentsatz:
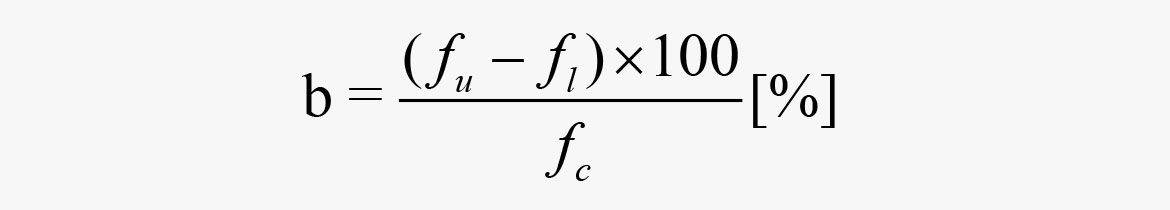
wobei
fu = obere Cutoff-Frequenz [Hz]
fl = untere Cutoff-Frequenz
fc = Mittenfrequenz [Hz]
Beispiel: (1/1 Oktave ~ 70%, 1/3 Oktave ~ 22%).
Q-Faktor
Der Q-Faktor eines Filters wird wie folgt berechnet:
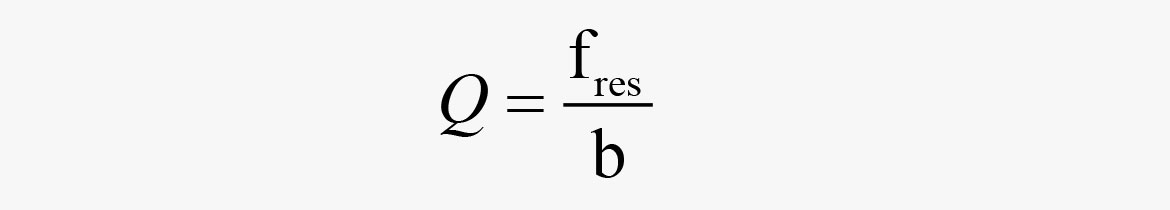
wobei
fres = Resonanz-/Mittenfrequenz [Hz]
b = Bandbreite[Hz]
Präfix bei Zahlen
Ein Präfix ist ein Zusatz, der einem Wort oder einer Zahl vorangestellt wird, um seine Bedeutung zu ändern. Ein Ziffernpräfix ist praktisch, da es das Verständnis extrem kleiner (oder extrem großer) Zahlen erleichtert.
Ein Präfix ersetzt die Potenzschreibweise. Zum Beispiel ist „2000“ gleich „2 mal 10 hoch 3“ oder wird als 2*103 geschrieben. Notiert mit Präfix: „2k“, wobei „k“ den Faktor 1000 angibt.
Hier eine Liste von numerischen Präfixen, wie sie vom SI-System definiert werden:
| Präfix | Abkürzung | Potenz | Wert |
| Tera | T | 1012 | 1 000 000 000 000 |
| Giga | G | 109 | 1 000 000 000 |
| Mega | M | 106 | 1 000 000 |
| Kilo | k | 103 | 1 000 |
| Hekto | h | 102 | 100 |
| Deka | da | 101 | 10 |
| Basiseinheit | - | 1 | 1 |
| Dezi | d | 10-1 | 0.1 |
| Zenti | c | 10-2 | 0.01 |
| Mikki | m | 10-3 | 0.001 |
| Mikro | µ | 10-6 | 0.000 001 |
| Nano | n | 10-9 | 0.000 000 001 |
| Piko | p | 10-12 | 0.000 000 000 001 |
Die Einheit für die Kapazität eines Kondensators ist Farad. Allerdings weisen Kondensatoren in der Praxis oft Werte auf, die nur ein kleiner Bruchteil der Basiseinheit darstellen, z.B. 0,0000000000022 Farad. Die lässt sich einfacher ausdrücken als 2,2 pF (Piko Farad).
Ein Widerstand mag einen Wert von 1000000 Ω besitzen, einfacher lässt sich das als „1 MΩ“ schreiben.
Oder ein Mikrofon weist eine Empfindlichkeit von 0,01V auf, einfacher geschrieben als „10 mV“.
Wenn wir über den barometrischen Druck in der Luft sprechen, bewegen wir uns im Bereich von 1000 hPa (Hektopascal), und nicht 1000 kPa, was nachvollziehbarer wäre. Allerdings scheint hier die frühere Tradition durch, Bar statt Pascal zu verwenden, denn 1000 Millibar = 1000 hPa.
Verwirrung bei allgemeiner Zählweise und Quantifizierung von Computerdaten
Bei der Berechnung der Größe von digitalen Informationen, die von Computern verarbeitet werden, muss man sich darüber im Klaren sein, dass alle Angaben auf Bytes [B] basieren, die jeweils 8 Bit enthalten. Somit wird die Anzahl der Bits pro Abtastwert ein Vielfaches von 8 (1 * 8, 2 * 8, 3 * 8, und so weiter). Die Anzahl an Bits pro Sample bei PCM Audio ist entweder 8 (1 Byte), 16 (2 Byte), 24 (3 Byte) oder 32 (4 Byte). Für eine höhere Auflösung und interne Verarbeitung können 64 Bit oder mehr gelten.
Da diese Datenmengen schnell groß werden, ist die Verwendung von Präfixen sinnvoll. Die Präfixeinheiten sind im SI-System definiert, darunter „k“ (Kilo), „M“ (Mega), „G“ (Giga) und T (Tera). Obwohl wir dieselben Präfixbezeichnungen verwenden, gilt die binäre Definition, sobald wir Dateigrößen beschreiben, was ziemlich verwirrend ist!
So werden die Dateigrößen berechnet, wie sie auf dem Computer angezeigt werden:
1 B = 8 Bit
1 kB = 1024 B = 8192 Bit
1 MB = 1024 kB = 8,388,608 Bit (≈ 8.39 * 106 Bit)
1 GB = 1024 MB ≈ 8.59 * 109 Bit
1 TB = 1024 GB ≈ 8.8 * 1012 Bit
Beispiel:
Wie viel Speicherkapazität wird für eine einstündige Stereo-Aufnahme bei 44,1 kHz / 16 Bit benötigt?
Die Anzahl erforderlicher Bit berechnet sich wie folgt:
Abtastfrequenz * Anzahl der Bit pro Sample * Anzahl der Audiokanäle * Dauer der Aufnahme (in Sekunden):
[1 Stunde = (60 min * 60 s) = 3600 s]
44,100 (Samples pro Sekunde) * 16 (Bit pro Sample) * 2 (Kanäle) * 3600 (Sekunden) = 5.08 * 109 Bit
Anzahl an Bytes: 5.08 * 109 / 8 = 6.35 * 108 B
Anzahl an kB: 6.35 * 108 / 1024 = 6.20 * 105 kB
Anzahl an MB: 6.20 * 105 / 1024 = 605.6 MB
Präfixe für binärbasierte Zahlen gibt es schon seit vielen Jahren. Einige Hersteller verwenden bei der Angabe ihrer Festplattenkapazität binäre Präfixe. In der folgenden Tabelle werden die dezimalen Präfixe mit den binären Präfixen nach der Definition der IEC (International Electrotechnical Commission) oder dem JEDEC (Joint Electron Device Engineering Council) verglichen.
| Dezimal | Binär | ||||||||
| Wert | SI | Wert | IEC | JEDEC | |||||
| Faktor | Symbol | Name | Faktor | Symbol | Name | Symbol | Name | ||
| 1000 | 103 | k | Kilo | 1024 | 210 | Ki | Kibi | K | Kilo |
| 10002 | 106 | M | Mega | 10242 | 220 | Mi | Mebi | M | Mega |
| 10003 | 109 | G | Giga | 10243 | 230 | Gi | Gibi | G | Giga |
| 10004 | 1012 | T | Tera | 10244 | 240 | Ti | Tebi | - | - |
| 10005 | 1015 | P | Peta | 10245 | 250 | Pi | Pebi | - | - |
| 10006 | 1018 | E | Exa | 10246 | 260 | Ei | Exbi | - | - |
| 10007 | 1021 | Z | Zetta | 10247 | 270 | Zi | Zebi | - | - |
| 10008 | 1024 | Y | Yotta | 10248 | 280 | Yi | Yyobi | - | - |
Tabelle: In dieser Tabelle werden dezimalbasierte Präfixe mit binärbasierten Präfixen verglichen.
Leider ist es oft üblich, Dezimalpräfixe zu verwenden, als wären sie binär.
In obiger Berechnung wäre das korrekte Ergebnis also 605,6 MiB.
Beachte, dass das Ki den Großbuchstaben K verwendet. Manchmal kann K (ohne das „i“) auch Ki bedeuten.
IEC 60027-2, Second edition, 2000-11: Letter symbols to be used in electrical technology - Part 2: Telecommunications and electronics.


